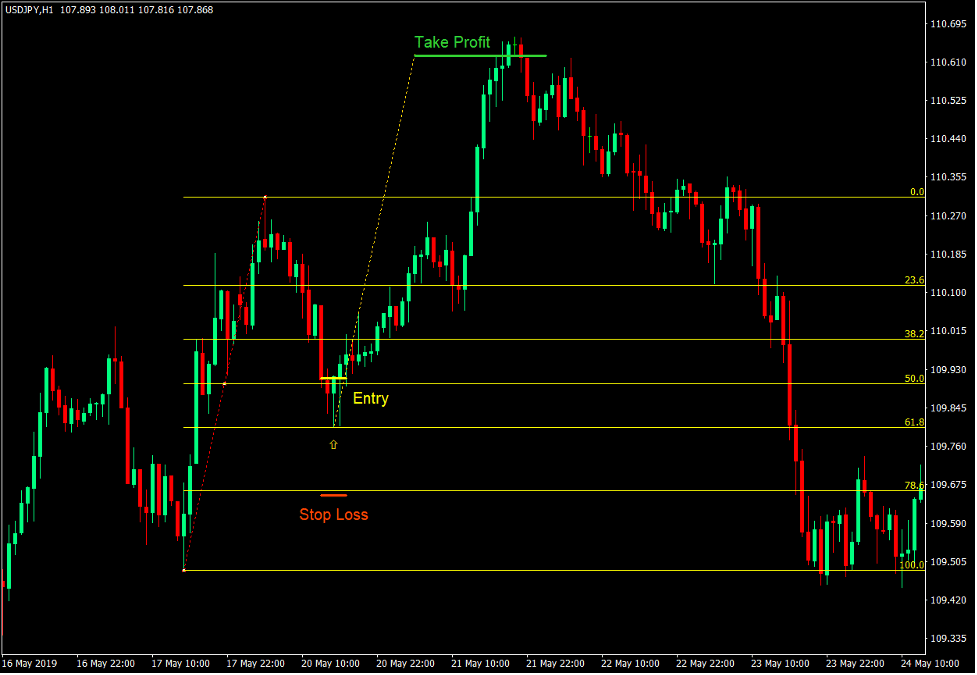
Traders are often on the look out for tools that would give them a trading edge. It may be an indicator, a charting tool, a trading strategy, basically anything that would give them an advantage over most traders in the market. For the most part, traders would often look for something novel in the hopes that their unique tool would give them the advantage they are looking for. However, most would forget that what matters most is that they have a tool that works. The Fibonacci Retracement tool is a basic trading tool which is found on all MT4 platforms, as well as other trading and charting platforms. In spite its being a basic tool, it is however very effective. Professional traders use them. Profitable traders use them. Big bank institutional traders use them. It would be a good idea if we would also discover what it is and how to use it effectively. Fibonacci Sequence and the Fibonacci Ratio The Fibonacci Sequence is was discovered by Leonardo of Pisa, also known as Fibonacci. Fibonacci was a mathematician who first studied with the Arabs and later on introduced algebra to Europe. Along with algebra, he also brought with him his observation of the Fibonacci Sequence. The Fibonacci Sequence is a series of numbers which has a core logic based on the addition of two sequential sums starting from 1. Starting from 1, the Fibonacci Sequence is as follows: 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, 5 + 8 = 13, 8 + 13 = 21, 13 + 21 = 34, 21 + 34 = 55, 34 + 55 = 89, 55 + 89 = 144, 89 + 144 = 233, and so on up to infinity. If you would observe the sequence closely, you would see that there are recurring patterns that can be found as you go along the sequence. This becomes apparent as the figures increase. For example, if you would divide the first addend by the second addend, you would note that the quotient is usually around 0.618. This means that the first addend is always 61.8% of the second addend. Inversely, the difference between the two addends would always be 38.2%. If you would also divide the sum by the second addend, the result would always be close to 1.618, meaning that the sum is always close to 161.8% of the second addend. We could also note that the sum is always close to 261.8% of the first addend. These percentage patterns, 38.2%, 61.8%, 161.8% and 261.8%, form the basic Fibonacci Ratios, with the ratio of 61.8% being the “Golden Ratio”. There are many more mathematical patterns that could be observed in this sequence. However, these percentages are the most basic Fibonacci Ratios. These ratios may not be interesting mathematically. What makes it more interesting is that these patterns are also recurring ratios in nature, be it the helix of a shell, the veins of a leaf, the human limbs or a fractal of a snowflake. What makes it even more interesting is that these same Fibonacci Ratio patterns have also been discovered by traders to be recurring ratios in a technical price chart. Fibonacci Ratios and the DiNapoli Levels Joe DiNapoli included the Fibonacci Ratios as one of the bases for a DiNapoli Level in his book “Trading with DiNapoli Levels: The Practical Application of Fibonacci Analysis to Investment Markets”. DiNapoli Levels are basically levels in which price typically bounce from. In his book, Joe DiNapoli outlined how price tends to bounce off certain Fibonacci Ratio levels based on swing points. He introduced there the idea that price tends to bounce off the 61.8% price point of the length of a price swing during trending markets. This 61.8% ratio has been known as the “Golden Ratio”. He noted that price typically bounces off 61.8% and would rarely reach 78.6%, which is one of the more intricate Fibonacci percentage ratios. He also noted that price would typically move in the direction of the trend usually by the same length as the prior price swing or 100%, 138.2%, or 161.8%. As such, his main trading strategy was to enter the market at 61.8% of the price swing, set a stop loss at 78.6%, and take profit at 100%, 138.2% or 161.8%. He also added levels 50% and 38.2% as potential points where price could also bounce off making it a valid entry level.